حل مسئله فروشنده دوره رد (tsp) با استفاده از الگوریتم ژنتیک

در حل TSP با الگوریتم ژنتیک سه قسمت اساسی Encoding ,  Mutation , Crossover است.

 روشهای  Encoding

1.استفاده از ماتریس مجاورت گراف است . اگر در مکان i , j عدد 1 وجود داشت یعنی یک یال از ذاس i به j وجود دارد و اگر 0 بود یعنی یالی یا مسیری نیست  به طور مثال 

در ماتریس روبرو از راس 1 به راس 3 میرویم و از راس 3 به راس 2 میرویم و از راس 2 به راس 1 میرویم در واقع این دور را ایجاد می کنیم:

1--->3--->2--->1

که برای راس یک می توان از 001 و برای راس دوم از 100 و برای راس سوم از 001 نیز استفاده کرد به جای استفاده از ماتریس.

2. استفاده از جایگشت است که در حل مسائل TSP بیشتر از این روش استفاده می شود که برای مثال بالا به این شکل مطرح می شود شماره هر راس را کنار هم قرار می دهیم    1321

جمعیت اولیه

با توجه به Encoding که انتخاب می کنیم تعدادی جمعیت اولیه را که می خواهیم از آن استفاده کنیم را ایجاد می کنیم.

تابع برازش یا Fitness برای آنها را نیز محاسبه می کنیم که برای TSP استاندارد طول دور حاصل از پیمایش در راستای کروموزوم های مورد نظر می باشد.

روشهای Crossover در TSP

یکی از نسائل مهم در TSP که به روش جایگشت encoding میشود مسئله Crossover می باشد زیرا بعد از عمل Crossover   فرزندان نیز باید خاصیت جایگشت بودن خود را حفظ کنند.

همانطور که ملا حظه می کنید بعضی اعداد دوبار تکرار شده و خاصیت جایگشتی اعداد 0 تا 7 را ندارد که به چند روش می توان این مشکل را حل کرد که در زیر به شرح چند روش آن خواهیم پرداخت:

1 - روش PMX

یک نقطه را به دلخواه در کروموزوم والد انتخاب می کنیم.

سپس قسمت های تکراری را در کروموزوم مقابل پیدا می کنیم و جای آنها را تعویض می کنیم.

و این کار را چند بار تکرار می کنیم تا فرزندان با ویژگیهای مختلف داشته باشیم.

2 - روش OX  (ordered Crossover)

در این روش نیمی از کروموزوم ها را ارپز والد اول انتخاب می کنیم و در همان جای خود در فرزند قرار می دهیم و بقیه کروموزمو ها فرزند را با توجه با والد دوم به ترتیب پر می کنیم مانند شکل زیر:

روش CX (cycle crossover)

برای توضیح این روش ابتدا از شکل شروع می کنیم فکر کنم این طور بهتر می توان توضیح داد:

از والد اول شروع می کنیم واولین عنصر را انتخاب می کنیم (عدد 1 ) حالا به اولین عنصر از والد دوم میرویم ( عدد 9) آنها را به هم وصل می کنیم در ادامه دنبال عدد 9 در والد اول میرگردیم  و آنها را به هم وصل می کنیم و دوباره به سمت عنصر والد دوم در همان مکان میرویم (عدد 4) و این کار را انچنان ادامه می دهیم تا به عنصر اولی که انتخاب کردیم یعنی 1 برسیم و دوباره عنصر بعد را که چرخه نیست میرویم (عدد2) و ینکار را ادامه میدهیم تا دوباره به آن برسیم و در دور بعد تنها یک عنصر باقیمانده (عدد6 ) و در پایان جای عناصر هر والد را با توجه به جهت های بدست آمده جابه جا می کنیم حالا دو فرزند جدید داریم.

روش MOX

ادامه دارد  ...

مساله فروشنده دوره گرد

مساله فروشنده دوره گرد   Traveling salesman Problem یا به اختصار TSP به این شکل است که یک فروشنده دوره گرد می خواهد در تعداد n شهردوری به وجود آورد که فروشنده از تمام شهر ها عبور کند و از تمام آنها فقط یک بار عبور کند و هزینه این دور نیز کمترین هزینه باشد.

منشا TSP دقیقا مشخص نیست ولی اولین نمونه شبیه به این مساله توسط اویلردر سال 1795 مطرح شده و به این صورت بود که یک مهره اسب می بایست روی صفحه شطرنج حرکت کند و از هر خانه دقیقا یکبار عبور کند.

 TSP را می توان به صورت ریاضی نیز مطرح کرد به صورت یگ گراف وزن دار G(v,e) که می خواهیم دوری فراگیربا مینیمم مجموع یالها  گذرنده را داشته باشیم.

که برای محاسبه آن نیاز داریم تا جایگشت های  n شهر متمایز و سپس ارزیابی هر حالت بررسی شود . که برای یافتن مینیمم دورها به حداکثر n! محاسبه احتیاج است ولی اگر تعداد n ها (شهرها)را زیاد در نظر بگیریم تعداد محاسبات بسیار زیاد خواهد بود.

 TSP جزء مسایل NP سخت است.مجموعهٔ «ان‌پی-سخت» شامل چندهزار مسئلهٔ مختلف با کاربردهای فراوان است که تاکنون برای آن‌ها راه حل سریع و قابل انجام در زمان معقول پیدا نشده‌است و به احتمال زیاد در آینده نیز یافت نخواهد شد.

بررسی پیچیدگی  TSP با یک مثال:

فرض کنیددر  نمودار زیر A , B  , C  , D   به عنوان 4 شهر که می خواهیم  از آن ها در یک دور عبور کنیم و آن کمترین مسافت را طی کنیم مسافت بین هر شهر را نیز بر اساس کیلومتر مشخص کرده ایم.

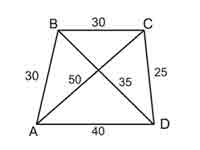
این مساله را می توان با نوشتن همه دورهای همیلتونی ممکن با نقطه شروع و پایان از راس و محاسبه کل مسافت پیموده شده برای هر دور حل کرد.

مسیر	مسافت
ABCDA ABDCA ACBDA ACDBA ADBCA ADCBA	125=30+30+25+40 30+35+25+50=140 50+30+35+40=155 140 155 125

بنابراین مسیر یا حداقل مسافت کل یعنی، 125 کیلومتر را به دست می دهد. حالت کلیTSP شامل یافتن یک دور همیلتونی برای یک گراف دلخواه راسی با حداقل مسافت پیموده شده است، که هر یال در آن مسافت بین دو راس را نشان می دهد. یک راه برای حل مساله، حالت کلی استفاده از روش مثال بالا است. برای این منظور،همه دورهای همیلتونی را که از یک راس خاص شروع شده و به همان راس پایان می یابد می نویسیم و مسافت کل هر دور را حساب می کنیم و از میان آنها، آن دوری را انتخاب می کنیم، که مسافت کل آن حداقل است، با این حال حتی برای مقادیر متوسط این روش غیر عملی است. مثلاً برای یک گراف کامل با 30 راس تعداد دور همیلتونی مختلف با شروع و پایان از یک راس خاص وجود دارد، که باید بررسی شود. حتی اگر برای هر دور پیدا شده در محاسبه مسافت کل به یک میکروثانیه زمان احتیاج باشد، برای 30 راس تقریباً سال نیاز داریم.

TSP بطور مستقیم در مرتبه زمانی(!O(n حل می شود اما اگر به روش برنامه نویسی پویا برای حل آن استفاده کنیم مرتبه زمانی آن (O(n^2*2^n خواهد شد که جز مرتبه های نمایی است. باید توجه داشت علی‌رغم آنکه مرتبه نمایی مذکور زمان بسیار بدی است اما همچنان بسیار بهتر از مرتبه فاکتوریل می باشد

راه حل TSP

سه روش کلی برای کد کردن راه حل های مسئله TSP ارائه شده است که در الگوریتم های مختلفی قابل استفاده هستند. راه حل های سه گاه عبارتند از:

الف) نمایش جواب به صورت رشته گسسته جایگشتی که در الگوریتم های زیر قابل استفاده است: الگوریتم ژنتیک یا Genetic Algorithms (به اختصار GA) شبیه سازی تبرید یا Simulated Annealing (به اختصار SA) جستجوی ممنوعه یا Tabu Search (به اختصار TS) جستجوی همسایگی متغیر یا Variable Neighborhood Search (به اختصار VNS) بهینه سازی کلونی مورچگان یا Ant Colony Optimization (به اختصار ACO) جستجوی هارمونی یا Harmony Search (به اختصار HS) و سایر الگوریتم های بهینه سازی گسسته

ب) نمایش جواب به صورت کلیدهای تصادفی یا Random Key که در الگوریتم های زیر قابل استفاده است: الگوریتم ژنتیک یا Genetic Algorithms (به اختصار GA) بهینه سازی ازدحام ذرات یا Particle Swarm Optimization (به اختصار PSO) الگوریتم رقابت استعماری یا Imperialist Competitive Algorithm (به اختصار ICA) تکامل تفاضلی یا Differential Evolution (به اختصار DE) بهینه سازی مبتنی بر جغرافیای زیستی یا Bio-geography Based Optimization (به اختصار BBO) استراتژی های تکاملی یا Evolution Strategies (به اختصار ES) برنامه ریزی تکاملی یا Evolutionary Programming (به اختصار EP) و سایر الگوریتم های بهینه سازی پیوسته

پ) نمایش جواب به شکل ماتریس های شبیه فرومون که توسط تمامی الگوریتم های اشاره شده در مورد (ب) قابل استفاده می باشد.

منابع:

مسئله فروشنده دوره گرد

مقاله ای در خصوص الگوریتم های ژنتیک و حل مسئله TSP

یک مثال ساده با الگوریتم ژنتیک

تابع f(x)=-X²+6X-3 را در نظر بگیرید.

می خواهیم مقدار ماکزیمم را برای بیابیم.

مراحل حل مسئله به روش الگوریتم ژنتیک

1) کد کردن

برای اینکار  چون ما می خواهیم اعداد بین 0 تا 15 را برای X مورد بررسی قرار دهیم پس بزگترین مقدار ما 15 هست که می توانیم آنرا به معادل باینری تبدیل کنیم که می شود 1111  یعنی حداکثر 4 بیت لازم داریم که می شود طول کروموزوم برای حل مسئله

2)تابع برازش

تابعی است که مقدار FINNESS را محاسبه می کند که از خود تابع F(X) استفاده می کنیم یعنی به ازای a , b اگر f(a) بزرگتر از f(b) باشد آنگاه a از b بهتر است.

3) انتخاب

فرض کنیم که در جمعیت اولیه:

3   ---->              0011                ----->            f(3)=6

8  ---->                1000                  ---->             f(8)=-19

4) ترکیب

فرض کنید که ترکیب عمل زیر را انجام می دهد

point 3       ---->  1000     ---->1001

point 3       ---->  0011     ---->0010

5) جهش

عمل جهش را نیز به صورت زیر انجام می دهیم

point 2     ---->  0010       -----> 0110=6

point 2     ---->  1001      -----> 1101=13

حال کروموزوم های متولد شده به جمعیت اولیه اضافه می شوند و دوباره جوابها با fitness  های پایین حذف می شوند برای اینکه جوابهایی مانند x=6 که بهترین جواب است در مراحل بعدی به نحوی از بین نرود بهترین جوابها را در جایی کنار می گذاریم

روشهایی مختلفی برای توقف الگوریتم وجود دارد مثلا اینکه اگر در طی چند مرحله جواب بهتری بدست نیامد و یا اینکه میانگین برازندگی جواب های موجود همان برازندگی بهترین جواب است

منبع : الگوریتم‌های ژنتیک و حل مسئله TSP

الگوریتم ژنتیک

الگوریتم ژنتیک     Genetic Algorithm   -   GA

تاریخچه:
مقوله ژنتیک توسط چارلز داروین در سال 1859 به طور جدی با بیان فرضیه تکامل مطرح شد و در سال 1903 کروموزوم به عنوان واحد وراثت معرفی گردید. در سال 1905 واژه ژنتیک توسط یک زیست شناس انگلیسی بنام ویلیام ویستون وضع گردید .
در سال 1927 واژه جهش برای بیان تغییرات فیزیکی در ژنها وضع شد و در سال 1931 واژه برش یا همبری وضع گردید.
در سال 1953 ساختار DNA  بطور کامل به شکل مارپیچی توسط جیمز واتسون و فرانسیس کریک توضیح داده شد که برای آن جایزه نوبل را نیز به ارمغان آورد.

مقدمه:
قانون فرضیه تکامل در طبیعت بدین صورت است که تنها گونه هایی از یک جمعیت ادامه نسل می دهند که بهترین خصوصیات را  داشته باشند و آنهایی که این خصوصیات را نداشته باشند به تدریج و در طی زمان از بین می روند.
در الگوریتم ژنتیک نحوه تکامل ژنتیکی موجودات زنده شبیه سازی می شود . این الگوریتم با الهام از روند تکامل طبیعی مسائل را حل می نماید .یعنی مانند طبیعت یک جمعیت از موجودات را تشکیل می دهند و با انجام اعمالی برروی این مجموعه یک مجموعه بهینه و یا موجودات بهینه دست می یابند.
الگوریتم‌های ژنتیک یکی از الگوریتم‌های جستجوی تصادفی است که در حل مسائل بهینه‌سازی کاربرد فراوانی دارند. به عنوان مثال می‌توان به مسئله فروشنده دوره گرد اشاره کرد.

واژه ها:
کروموزوم: در الگوریتم ژنتیک، یک کروموزوم مجموعه‌ای از پارامترهاست به طوری که یک راه حل پیشنهادی را برای مسئله‌ای که الگوریتم ژنتیک سعی در حل آن دارد، تعریف می‌نماید. یک کروموزوم بسته به مسئله می تواند، رشته ای از متغیرهای گسسته، مقادیر دودویی و مقادیر پیوسته باشد.
جمعیت : الگوریتم ژنتیک بوسیله مجموعه ای ار کروموزوم ها شروع به مار می کند.
اعضای این مجموعه معمولاً به صورت تصادفی انتخاب می‌شوند اما در الگوریتم‌های بهینه، از قیدهایی استفاده می‌شود تا جمعیت پراکندگی بیش از حد نداشته باشد.
بیت : بیت در یک رشته همان نقش ژن در طبیعت را دارد.
فنو تایپ: هر کروموزوم متناظر با مجموعه جوابی برای مسئله است
فضای جستجو : بر اساس اصل ادامه حیات بهترین ها و تکثیر نوع برتر پی ریزی شده است .(هدف پیدا کردن بهترین جواب از میان جوابهای مختلف)

تابع برازش Fitness
برای اینکه بتوانیم موجودات بهتر را درون جمعیت شناسایی کنیم بایستی معیاری را تعریف کنیم که بر اساس آن موجودات بهتر را تشخیص دهیم . ارزیابی اینگونه است که بر حسب اینکه موجود چقدر خوب است یک عدد به آن نسبت می دهیم این برای مو جودات بهتر بزرگتر (MAX) و یا کوچکتر (MIN) است را شایستگی  آن موجود می نامیم

الگوریتم ژنتیک
روش متداول پیاده سازی الگوریتم ژنتیک بدین ترتیب است:
مجموعه ای از کروموزوم ها (افراد)که جمعیت نامیده می شود تولید و به طور متناوب با کروموزوم های جدید جایگزین میشوند.
در هر بار تکرار تمامی کروموزوم ها (فرضیه ها) با استفاده از تابع برازش fitness  مورد ارزیابی قرار می گیرد آنگاه تعدادی ار بهترین آنها با استفاده از این تابع انتخاب می شود و جمعیت جدید را تشکیل می دهد.
تعدادی از این فرضیه های انتخاب شده به همان صورت مورد استفاده قرار می گیرد و ما بقی با استفاده از اپراتورهای ژنتیکی نظیر Crossover  و Mutation  برای تولید فرزندان بکار می رود.

عملگرهای الگوریتم ژنتیک
Encoding
الگوریتم ژنتیک به جای این که بر روی پارامتر ها یا متغیر های مساله کار کند با شکل کد شده آنها سرو کار دارد. یکی از روشهای کد کردن ، کد کردن دودویی می باشد.

Evaluation
تابع برازندگی این تابع هر رشته را با یک مقدار عددی ارزیابی می کند

Crossover ( ادغام )
مهمترین عملگر در الگوریتم ژنتیک عملگر ترکیب است . ترکیب ، فرآیندی است که در آن نسل قدیمی کروموزوم ها با یکدیگرمخلوط و ترکیب می شوند تا نسل جدیدی بوجود آورند
اپراتور Crossover با استفاده از دو  رشته والد دو رشته فرزند بوجود میآورد.
برای اینکار قسمتی از بیتهای والدین در بیتهای فرزندان کپی میشود.
انتخاب بیت هائی که باید از هر یک از والدین کپی شوند به روشهای مختلف انجام میشود
single-point crossover

Two-point crossover

Uniform crossover

برای تعیین محل بیتهای کپی شونده از یک رشته به نام Crossover Mask  استفاده میشود

 

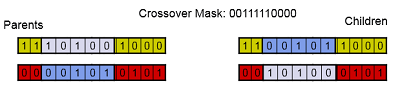
Mutation(جهش)
جهش نیز عملگری است که جوا بهای ممکن دیگری را متولد می کند . که در جهش ممکن است ژنی از مجموعه ژن ها حذف و با ژنی که تا به حال وجود نداشته به آن اضافه شود.
اپراتور mutation  برای بوجود آوردن فرزند فقط از یک والد استفاده میکند. اینکار با انجام تغییرات کوچکی در رشته اولیه  بوقوع میپیوندد.
با استفاده از یک توزیع یکنواخت یک بیت بصورت تصادفی اتنخاب و مقدار آن تغییر پیدا میکند.

Decoding(رمز گشایی)
عکس عمل encoding  است . جواب ها را رمز گشایی می کنیم تا به نسخه واقعی جواب برسیم.

چارت الگوریتم ژنتیک

روشهای کد کردن:
کدینگ باینری :
هدف تبدیل جواب مسئله به رشته‌ای از اعداد باینری است.

کدینگ جایگشتی:
کروموزوم‌ها به صورت رشته‌ای از اعداد طبیعی نشان داده می‌شوند که هرکدام از این اعداد، مربوط به پارامتر ویژه‌ای در فضای حلّ مسئله است.

کدینگ مقدار:
کروموزوم‌ها می‌توانند هر نوع داده مرتبط با مسئله را در رشتۀ خود اختیار نمایند. به بعضی ژن‌ها بطور تصادفی عددی اضافه شده یا از آنها کم می‌گردد.

کدینگ درختی:
در این نوع کد گذاری یک درخت دودویی برای عبارت (کروموزوم) تشکیل می‌دهیم که معادل درخت پارس است و تمام اعمال مربوط به درخت پارس بر روی درخت قابل انجام است.این روش در نرم افزارهایی که تحت عنوان «کدهای الگوریتم ژنتیک» برای یک مسئلۀ خاص نوشته می‌شوند استفاده می‌شود. «لیسپ»

 
روش‌های انتخاب: Selection

• انتخاب چرخ رولت
• انتخاب ترتیبی
• انتخاب بولتزمن
• انتخاب حالت پایدار
• نخبه سالاری
• انتخاب رقابتی
• انتخاب قطع سر
• انتخاب قطعی بریندل
• انتخاب جایگزینی نسلی اصلاح شده
• انتخاب مسابقه
• انتخاب مسابقه تصادفی

منبع مطالب:

الگوریتم های فرا اکتشافی جستجو - الگوریتم های ژنتیک - مصطفی عباسی کیا