مساله فروشنده دوره گرد

مساله فروشنده دوره گرد   Traveling salesman Problem یا به اختصار TSP به این شکل است که یک فروشنده دوره گرد می خواهد در تعداد n شهردوری به وجود آورد که فروشنده از تمام شهر ها عبور کند و از تمام آنها فقط یک بار عبور کند و هزینه این دور نیز کمترین هزینه باشد.

منشا TSP دقیقا مشخص نیست ولی اولین نمونه شبیه به این مساله توسط اویلردر سال 1795 مطرح شده و به این صورت بود که یک مهره اسب می بایست روی صفحه شطرنج حرکت کند و از هر خانه دقیقا یکبار عبور کند.

 TSP را می توان به صورت ریاضی نیز مطرح کرد به صورت یگ گراف وزن دار G(v,e) که می خواهیم دوری فراگیربا مینیمم مجموع یالها  گذرنده را داشته باشیم.

که برای محاسبه آن نیاز داریم تا جایگشت های  n شهر متمایز و سپس ارزیابی هر حالت بررسی شود . که برای یافتن مینیمم دورها به حداکثر n! محاسبه احتیاج است ولی اگر تعداد n ها (شهرها)را زیاد در نظر بگیریم تعداد محاسبات بسیار زیاد خواهد بود.

 TSP جزء مسایل NP سخت است.مجموعهٔ «ان‌پی-سخت» شامل چندهزار مسئلهٔ مختلف با کاربردهای فراوان است که تاکنون برای آن‌ها راه حل سریع و قابل انجام در زمان معقول پیدا نشده‌است و به احتمال زیاد در آینده نیز یافت نخواهد شد.

بررسی پیچیدگی  TSP با یک مثال:

فرض کنیددر  نمودار زیر A , B  , C  , D   به عنوان 4 شهر که می خواهیم  از آن ها در یک دور عبور کنیم و آن کمترین مسافت را طی کنیم مسافت بین هر شهر را نیز بر اساس کیلومتر مشخص کرده ایم.

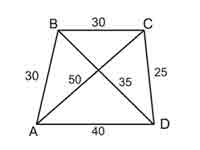
این مساله را می توان با نوشتن همه دورهای همیلتونی ممکن با نقطه شروع و پایان از راس و محاسبه کل مسافت پیموده شده برای هر دور حل کرد.

مسیر	مسافت
ABCDA ABDCA ACBDA ACDBA ADBCA ADCBA	125=30+30+25+40 30+35+25+50=140 50+30+35+40=155 140 155 125

بنابراین مسیر یا حداقل مسافت کل یعنی، 125 کیلومتر را به دست می دهد. حالت کلیTSP شامل یافتن یک دور همیلتونی برای یک گراف دلخواه راسی با حداقل مسافت پیموده شده است، که هر یال در آن مسافت بین دو راس را نشان می دهد. یک راه برای حل مساله، حالت کلی استفاده از روش مثال بالا است. برای این منظور،همه دورهای همیلتونی را که از یک راس خاص شروع شده و به همان راس پایان می یابد می نویسیم و مسافت کل هر دور را حساب می کنیم و از میان آنها، آن دوری را انتخاب می کنیم، که مسافت کل آن حداقل است، با این حال حتی برای مقادیر متوسط این روش غیر عملی است. مثلاً برای یک گراف کامل با 30 راس تعداد دور همیلتونی مختلف با شروع و پایان از یک راس خاص وجود دارد، که باید بررسی شود. حتی اگر برای هر دور پیدا شده در محاسبه مسافت کل به یک میکروثانیه زمان احتیاج باشد، برای 30 راس تقریباً سال نیاز داریم.

TSP بطور مستقیم در مرتبه زمانی(!O(n حل می شود اما اگر به روش برنامه نویسی پویا برای حل آن استفاده کنیم مرتبه زمانی آن (O(n^2*2^n خواهد شد که جز مرتبه های نمایی است. باید توجه داشت علی‌رغم آنکه مرتبه نمایی مذکور زمان بسیار بدی است اما همچنان بسیار بهتر از مرتبه فاکتوریل می باشد

راه حل TSP

سه روش کلی برای کد کردن راه حل های مسئله TSP ارائه شده است که در الگوریتم های مختلفی قابل استفاده هستند. راه حل های سه گاه عبارتند از:

الف) نمایش جواب به صورت رشته گسسته جایگشتی که در الگوریتم های زیر قابل استفاده است: الگوریتم ژنتیک یا Genetic Algorithms (به اختصار GA) شبیه سازی تبرید یا Simulated Annealing (به اختصار SA) جستجوی ممنوعه یا Tabu Search (به اختصار TS) جستجوی همسایگی متغیر یا Variable Neighborhood Search (به اختصار VNS) بهینه سازی کلونی مورچگان یا Ant Colony Optimization (به اختصار ACO) جستجوی هارمونی یا Harmony Search (به اختصار HS) و سایر الگوریتم های بهینه سازی گسسته

ب) نمایش جواب به صورت کلیدهای تصادفی یا Random Key که در الگوریتم های زیر قابل استفاده است: الگوریتم ژنتیک یا Genetic Algorithms (به اختصار GA) بهینه سازی ازدحام ذرات یا Particle Swarm Optimization (به اختصار PSO) الگوریتم رقابت استعماری یا Imperialist Competitive Algorithm (به اختصار ICA) تکامل تفاضلی یا Differential Evolution (به اختصار DE) بهینه سازی مبتنی بر جغرافیای زیستی یا Bio-geography Based Optimization (به اختصار BBO) استراتژی های تکاملی یا Evolution Strategies (به اختصار ES) برنامه ریزی تکاملی یا Evolutionary Programming (به اختصار EP) و سایر الگوریتم های بهینه سازی پیوسته

پ) نمایش جواب به شکل ماتریس های شبیه فرومون که توسط تمامی الگوریتم های اشاره شده در مورد (ب) قابل استفاده می باشد.

منابع:

مسئله فروشنده دوره گرد

مقاله ای در خصوص الگوریتم های ژنتیک و حل مسئله TSP